2의 보수(Two’s complement)

컴퓨터에서 2의보수가 어디에 쓰일까?
컴퓨터는 덧셈밖에 못합니다. 그렇다면 뺄셈이 덧셈을 통해서 연산을 하는데 이때 사용되는것이 보수입니다.
보수란?
보충을 해주는 수를 말합니다. 즉 3에 대한 10의 보수는 7, 7에 대한 15의 보수는 8 이런 식으로 어떠한 수가 N이 되기 위해 필요한 수를 말합니다.
보수로 뺄셈 구하는 법
사람이 쉽게 이해하려면 10진법으로 예를 들면 편합니다. 예를 들어 10 - 4를 구하려고 할때 사람이 보면 10에서 4를 빼면 6이 나오니까 답이 바로 나올겁니다.
하지만 컴퓨터는 덧셈만 가능합니다. 여기서 보수를 사용하면 덧셈을 통해 구할 수 있습니다.
4에 대한 10의 보수는 6, 즉 4 대신 보수를 사용해서 더한다 10 + 6이 됩니다. 10 + 6 = 16 여기서 컴퓨터는 1의 자리 숫자인 6만 보고 10의 자리 숫자는 버립니다.
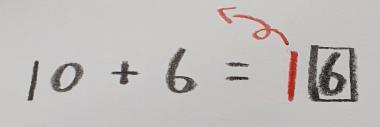
이렇게 숫자가 버려지는 과정을 오버플로라고 합니다.
오버플로 과정을 더 자세히 보면은 아래와 같이 됩니다.

그래서 컴퓨터는 -4를 메모리에 저장할때 6으로 저장합니다. 지금까지는 10진수로 예를 들었고 실제 컴퓨터에서 사용되는 2진수는 어떻게 되는지 알아 보겠습니다. (10진수랑 별 다를게 없음)
그 전에 컴퓨터에서 부호를 가진 2진수가 어떻게 이루어져 있는지 알아야 합니다.
컴퓨터에서 부호를 가진 정수 표현법
컴퓨터 내부에서는 +, - 기호를 모두 2진수로 표현해야 합니다. 즉 부호가 필요없는 +는 0, 부호가 필요한 -는 1 이렇게 표현합니다.
Byte단위로 예를 들면서 보면은 만약 10을 저장해야 한다면 메모리에 00001010 으로 저장 될것입니다. 즉, 맨앞의 비트는 양수임을 표현해야 되므로 0이고 나머지 7비트로 수를 표현합니다.
그럼 -8은 어떻게 저장될까요?
앞에 말했던 것처럼 뺄셈을 할 때는 보수를 저장합니다. 그러면 8을 2진수로 바꾸면 00001000입니다. 00001000의 2의보수는 11111000이 됩니다. 즉, 메모리에는 11111000으로 저장이 됩니다.
컴퓨터의 연산
그럼 10 - 8은 컴퓨터는 00001010 + 11111000으로 연산합니다. 00001010 + 11111000 = 100000010이지만 byte단위이기 때문에 오버플로가 발생해서 00000010의 값이 나옵니다.
표현 가능한 수의 범위(8비트)
| 양수 | 2진수 | 음수 | 2진수 |
|---|---|---|---|
| 0 | 00000000 | 0 | 00000000 |
| 1 | 00000001 | -1 | 11111111 |
| 2 | 00000010 | -2 | 11111110 |
| 3 | 00000011 | -3 | 11111101 |
| 4 | 00000100 | -4 | 11111100 |
| 5 | 00000101 | -5 | 11111011 |
| 6 | 00000110 | -6 | 11111010 |
| 125 | 01111101 | -125 | 10000011 |
| 126 | 01111110 | -126 | 10000010 |
| 127 | 01111111 | -127 | 10000001 |
| … | … | -128 | 10000000 |
음수가 하나 더 표현 할 수 있는 이유는 0이 양수쪽으로 한자리를 차지하기때문에 음수가 하나 더 표현 할 수 있습니다.(그렇다고 0이 양수라는건 아니다)

Leave a comment