부동소수점(Floating Point)
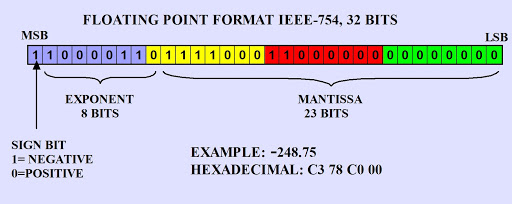
위의 사진과 같이 컴퓨터가 실수를 저장하는 방법입니다(32비트기준). 그럼 저 부동 소수점에 대해서 더 자세히 알아보겠습니다.
정규화된 과학적 표기법
컴퓨터는 정규화된 과확적 표기법의 가수와 지수를 이용하여 부동소수점을 표현합니다.
정규화된 과학적 표기법은 유효숫자들을 사용해 표현을 합니다.
유효숫자
수의 정밀도와 정확도에 영향을 주는 숫자들을 말합니다.
유효숫자의 조건
- 0이 아닌 수는 유효숫자
- 0이 아닌 두수사이에 있는 0은 유효숫자
- 소수점 아래에 왼쪽에 있는 0들을 뺀 나머지 유효숫자
예)
- 495의 유효숫자는 4, 9, 5
- 12300의 유효숫자는 1, 2, 3
- 1034의 유효숫자는 1, 0, 3, 4
- 0.0001049의 유효숫자는 1, 0, 4, 9
이렇게 유효숫자들을 가지고 어떻게 정규화된 과학적 표기법을 하는지 알아보겠습니다.
정규화된 과학적 표기법으로 바꾸는 방법
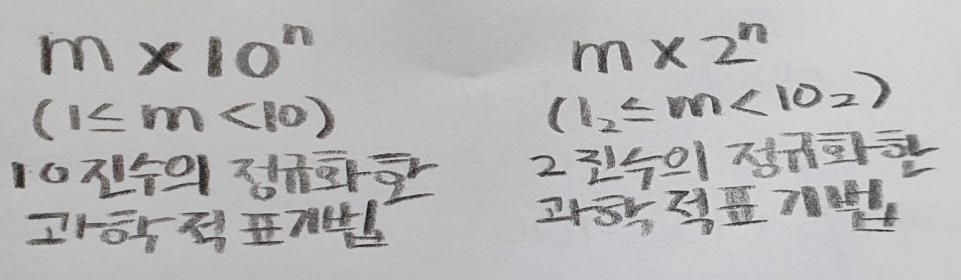
이와 같이 m에는 유효숫자들로만 이루어져 있습니다. m을 가수라고 하고 n을 지수라고 부릅니다.
예)
- 10진수 323456700의 정규화한 과학적 표기법은 3.234567 * 10^8이 됩니다.
- 가수는 3.234567이 되고 지수는 8이 됩니다.
- 2진수 110110.101의 정규화한 과학적 표기법은 1.10110101 * 2^5가 됩니다.
- 가수는 1.10110101이 되고 지수는 5가 됩니다.
2진수의 가수에서 정수부분은 항상 1이 올 수 밖에 없습니다.
그럼 이 정규화된 과학적 표기법을 32비트 부동소수점(IEEE 754)에 어떻게 사용되는지 알아보겠습니다.
부동소수점 비트

컴퓨터에서 부동소수점을 비트에 저장하려면 부호비트(Sign 1 Bit), 지수비트(Exponent 8 Bit), 가수비트(Mantissa 23 Bit)가 있어야 합니다.
- 부호비트: 음수면 1, 양수면 0 으로 이루어진 1비트
- 지수비트: 8비트로 이루어져 있고 양수, 음수표현이 가능
- 실제 지수에 127을 더해서 지수 비트에 저장하면 양수, 음수를 구분가능(128 이상은 양수, 127 미만은 음수, 127은 0) 예) 1010.10101과 -1010.10101 각각의 비트에 어떻게 저장되는지 알아보겠습니다.

두 수가 부호비트만 다르고 나머지는 같은걸 볼 수 있습니다.
지수비트는 양수, 음수를 구분하기 위해 3 + 127을 2진수로 바꿔서 저장한 것입니다.(지수비트를 실제비트로 만들려면 지수비트값 - 127하면된다) 가수비트는 맨 앞에 1이 빠져서 저장된 것이 보이는데 그 이유는 2진수의 가수의 정수부분은 항상 1이여서 저장 할 필요가 없기 때문입니다.
그럼 부동소수점 비트에 있는 값을 10진수로 변환하는 방법에 대해서 알아보겠습니다.
부동소수점 비트 10진수로 변환

위의 부동소수점 비트를 10진수를 변환하는 공식이 있습니다.
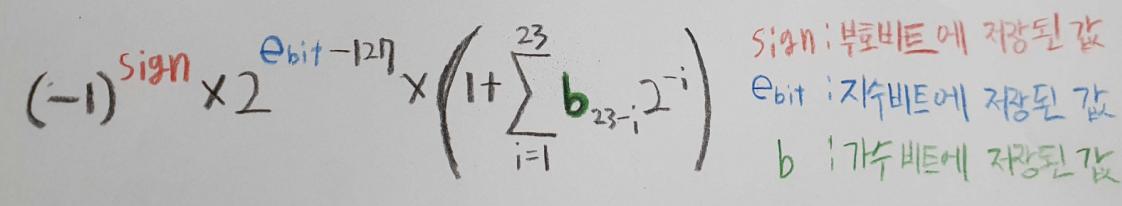
공식을 적용하면은
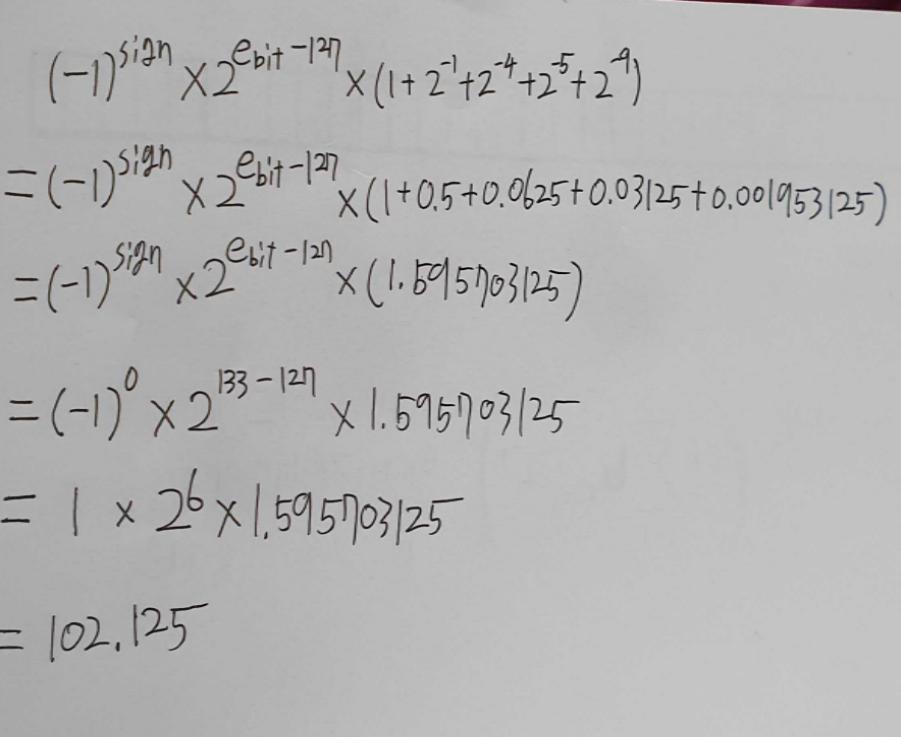
즉, 저 위의 부동소수점 비트는 102.125의 값을 저장하고 있는 겁니다.
지수범위
지수의 표현가능한 범위는 -126 ~ 127입니다. -127과 128을 포함 안 시킨 이유는
모든 지수비트가 0일때와 1일때는 특별하게 처리되기 때문입니다.
만약 지수비트가 0일때는
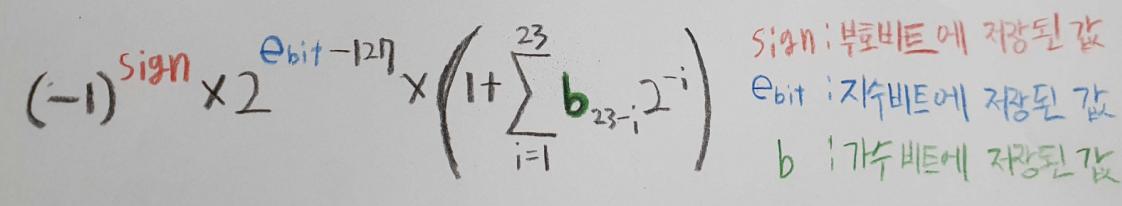
이 공식으로는 0.0이 절때 안나옵니다. 그래서 이때는 다른공식을 쓰는데 그 공식이 아래의 사진입니다.
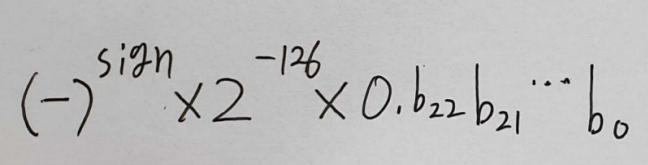
위의 공식은 0에 더 가까운 수를 표현하기 위한 공식 입니다.
모든 지수비트가 1일때는 가수비트에 따라 두가지로 정의됩니다.
만약 모든 지수비트가 1(0xFF)일때 모든 가수비트가 0(0x00)이면
- 무한대로 정의
- infinite
만약 모든지수비트가 1(0xFF)일때 모든 가수비트가 0이 아닐때면
- 수가 아님 NaN
- NaN은 잘못된 계산 실수로 표현 할 수 없는 값
정리
지수비트와 가수비트에 따른 계산식을 정리하면 아래의 표가 나옵니다.
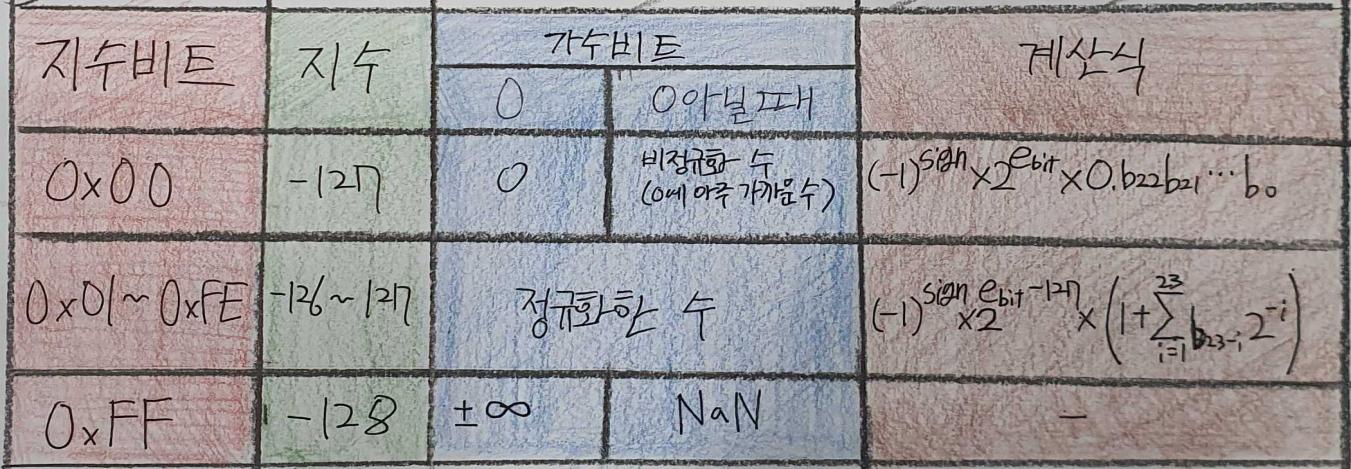

Leave a comment